logistic回归

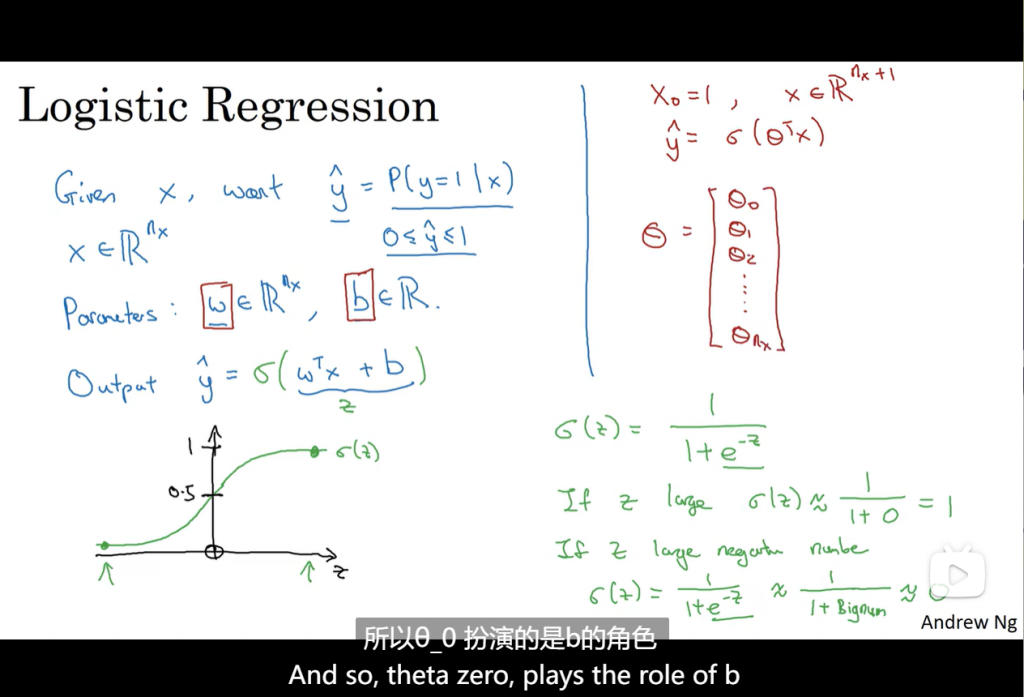
给定向量X，希望输出概率y_hat，X为n_x维向量，用sigmoid函数控制输出在0-1之间。学习W和b。

损失函数衡量训练的情况，在logist回归中，如果定义损失函数为：

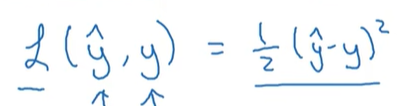
学习时的优化问题是非凸的，梯度下降法可能找不到全局最优解。

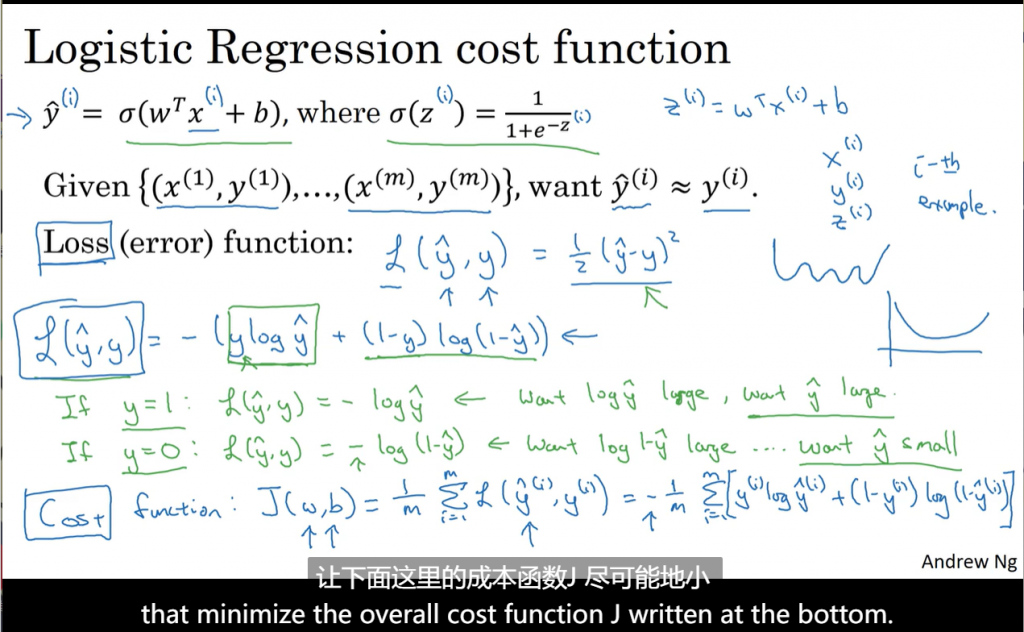
logistic回归通常用下面这个损失函数：

成本函数：

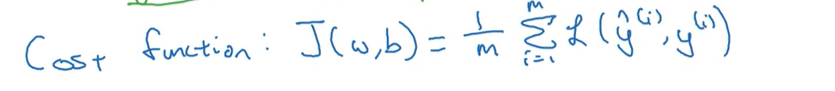
所有训练样本的损失函数平均值。

损失函数只适用于单个训练样本，成本函数则基于参数的总成本。所以训练时找到合适的W和b使得J尽可能的小。

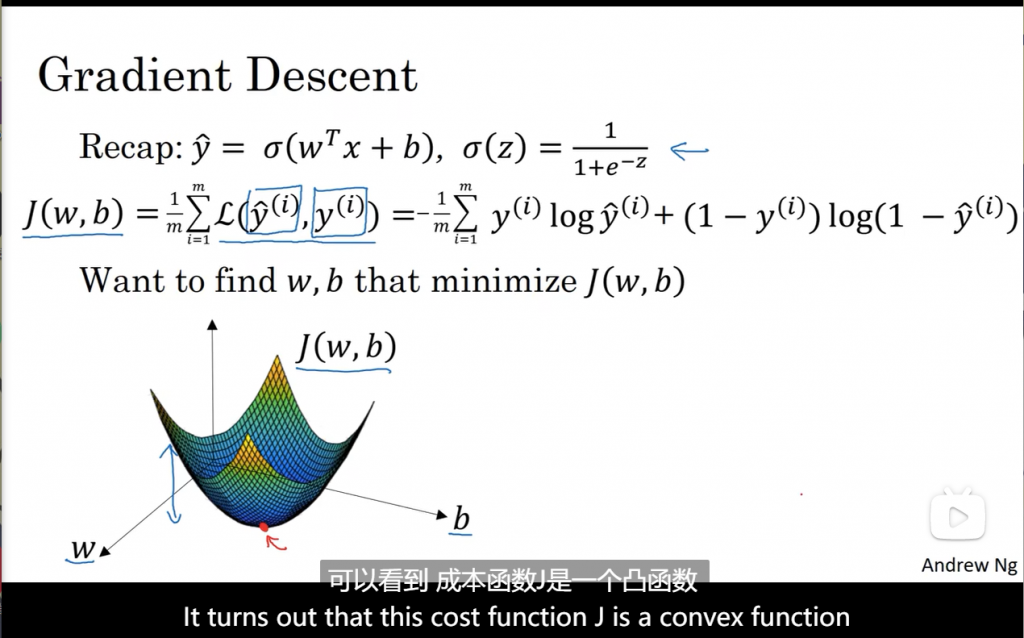
梯度下降法做的就是，从初始点开始，朝最陡的下坡方向走一步，在梯度下降一步后，或许在那里停下。因为它正试图沿着最快下降方向往下走。

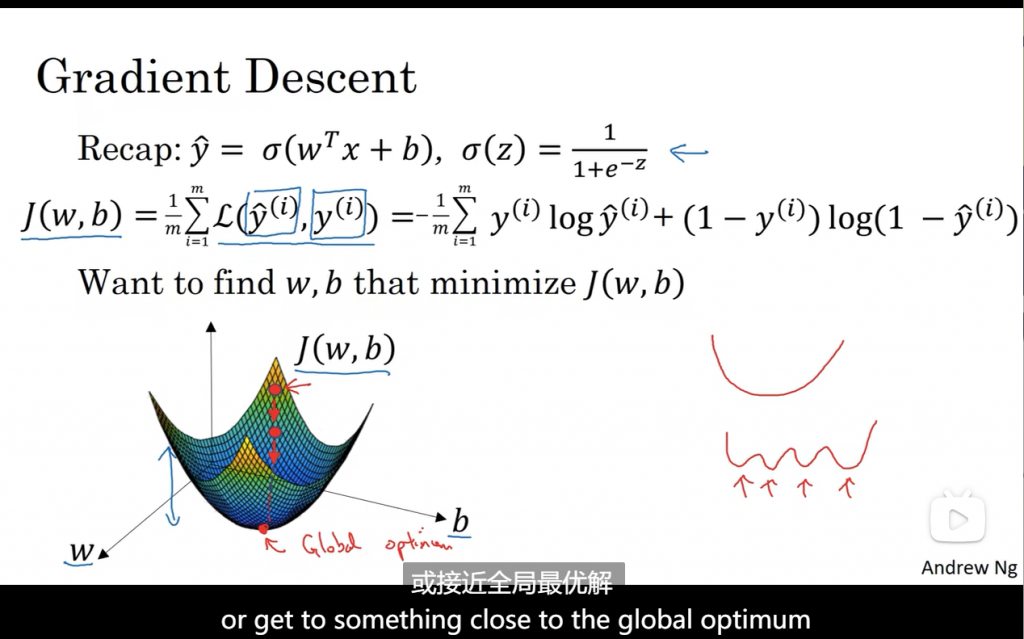
无论是在左边还是右边，都会往最小值方向走。

微积分细节不做笔记

计算图：

本质上就是链式法则

在这个例子中就是改变w1和w2使得Loss尽可能的小

这是单个样本的一次梯度更新计算过程

多个样本成本函数求偏导本质上是每个样本损失函数求偏导取平均值。

这是所有样本的一次梯度下降过程。使用双层循环比较低效，因此一般使用向量化技术。

向量化技术：2.11

to be continue。。。