（转）human3.6m数据集格式解析

最近做3d人体姿态骨骼相关的实验，需要使用到human3.6m这个数据集，但是这个数据集的格式以及使用方式在网上并没有人详细地进行说明，因此我记录下我对这个数据集的格式理解的过程。对于用xyz表示的格式不在赘述，但是在人体骨架运动序列的生成任务中，往往会采用李群和李代数的方法表示骨架，关于李群和李代数可以参考网上的其他博文，这里只叙述h36m数据是如何使用李代数表示人体骨架。

0.0000000,0.0000000,0.0000000,-0.0000000,-0.0000001,0.0000001,0.3230213,-0.4831149,-0.0673216,-0.0632727,-0.0000000,-0.0000000,-0.0513711,0.5105966,-0.0717521,0.3066142,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,0.3265765,0.3157165,-0.0472587,-0.1024184,-0.0000000,-0.0000000,0.0504554,-0.3802582,-0.0118426,0.2074713,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,0.4935718,0.0160918,-0.1225905,-0.0910649,0.0319310,0.0919449,-0.5382497,0.0032421,-0.3011716,1.3627026,-0.0115682,0.1639829,-0.0000000,-0.0000000,-0.0000000,-0.1539563,-0.0657004,2.0724664,-0.1472652,-0.2662845,0.7816223,-0.1515370,-0.0000000,-0.0000000,0.2704134,-0.5088616,0.1476415,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,0.0520571,0.0791909,-2.1037283,-0.1340761,0.4897867,-0.8238848,-0.3317853,-0.0000000,-0.0000000,0.1473034,-0.1267874,-0.0072563,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000
-0.0566091,-0.0728046,-0.4761781,0.0002633,-0.0016594,0.0013396,0.3249512,-0.4825976,-0.0681018,-0.0664033,-0.0000000,-0.0000000,-0.0504344,0.5090697,-0.0757788,0.3075081,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,0.3277222,0.3166970,-0.0482386,-0.1038797,-0.0000000,-0.0000000,0.0504261,-0.3792894,-0.0117432,0.2074303,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,0.4898341,0.0168204,-0.1218890,-0.0900892,0.0323371,0.0876651,-0.5319070,0.0068988,-0.3015916,1.3708540,-0.0113818,0.1643514,-0.0000000,-0.0000000,-0.0000000,-0.1516332,-0.0658906,2.0727837,-0.1523688,-0.3035229,0.7762181,-0.1673595,-0.0000000,-0.0000000,0.2622762,-0.4809161,0.1241033,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,0.0526290,0.0793313,-2.1033485,-0.1298485,0.4750284,-0.8241772,-0.3224269,-0.0000000,-0.0000000,0.1390186,-0.0978035,-0.0031509,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000,-0.0000000

由于数据繁多，我截取了两行作为例子。human3.6m对于文本中的每一行的定义是一帧中的标注，因此一个标注文件对应的视频有多少帧，这个文件就有多少行。其中每一行里面有99个数据，每三个数据为一组，共同组成一个旋转向量。

旋转向量简单的来说，就是若从向量a旋转到向量b，旋转向量的方向就是a和b旋转面的法向量的方向，旋转向量的大小对应a旋转到b的角度。

把这99个数据3个为一组，共分为33个旋转向量。

接下来说明这些旋转向量对应的关节以及human3.6m标注的数据结构。

h3.6m数据里，有个初始的人体骨骼模型，它简单的定义了各个骨骼边的长度以及它们之间的互相连接关系。下图是已经转换完成的骨骼图像，试想把图中旋转的角度全部去除，就能得到一个呆板的类似机器人的人体骨骼模型，那就是h3.6m假设的初始模型，当然具体h36m定义的并不像机器人，但是基本原理是一样的。

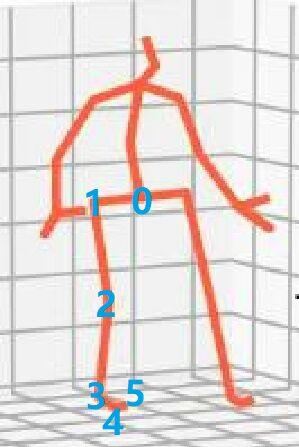
下面用数字i表示第i个旋转旋转向量，j-k表示人体骨骼上的一条向量边，则j-k在初始模型中有一条与之对应的边：

向量0在目前已看到的代码中没有看到使用的，用途不明，因此我也不把它叫做旋转向量。

旋转向量1：向量0-1的原始向量对应的旋转向量，也就是说原始向量经过旋转之后的到向量0-1；

旋转向量2：向量1-2的原始向量经过了旋转向量1旋转之后，在经过旋转向量2的旋转才能得到向量1-2，也就是说1-2的原始向量分别经过了旋转向量1和旋转向量2得到了图中的1-2；

具体原理可以去了解3d图形学中的世界坐标与相对坐标；

以此类推，这些旋转向量就组成了一条旋转链。

h36m中共有5条旋转链，分别是

0-1-2-3-4-5

0-6-7-8-9-10

0-11-12-13-14-15

12-16-17-18-19-20-21

|-22

12-24-25-26-27-28-29

|-30

附上全部关节点的标注顺序

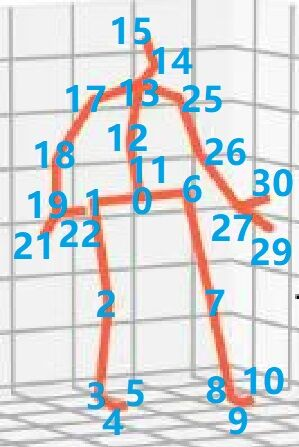
在h3.6m中，会有一些看似冗余标注点，如图中的11和0是重合的，其实是因为h36m的节点来说，如果它们的父节点相同，那么它们共享同一个旋转向量，因此所有父节点相同的节点相对父节点旋转角度都是一样的，这样会造成一些问题，比如节点0有3子节点，但是胯部的方向和脊椎的旋转方向是不一样的，因此就需要一个多设置一个11节点作为12的父节点来改变12节点的旋转方向。同理，20与19重合用来改变21的方向，28与27重合用来改变29的方向，16和24都与13重合，16用来改变17的方向，24用来改变25的方向，剩下的23和31则为无意义节点。

在所有可视化h36m的脚本中，都会有这么几组数据：

    parent = np.array([0, 1, 2, 3, 4, 5, 1, 7, 8, 9, 10, 1, 12, 13, 14, 15, 13,
                       17, 18, 19, 20, 21, 20, 23, 13, 25, 26, 27, 28, 29, 28, 31]) - 1

    offset = np.array([[0., 0., 0.],
                       [-132.95, 0., 0.],
                       [0., -442.89, 0.],
                       [0., -454.21, 0.],
                       [0., 0., 162.77],
                       [0., 0., 75.],
                       [132.95, 0., 0.],
                       [0., -442.89, 0.],
                       [0., -454.21, 0.],
                       [0., 0., 162.77],
                       [0., 0., 75.],
                       [0., 0., 0.],
                       [0., 233.38, 0.],
                       [0., 257.08, 0.],
                       [0., 121.13, 0.],
                       [0., 115., 0.],
                       [0., 257.08, 0.],
                       [0., 151.03, 0.],
                       [0., 278.88, 0.],
                       [0., 251.73, 0.],
                       [0., 0., 0.],
                       [0., 0., 100.],
                       [0., 137.5, 0.],
                       [0., 0., 0.],
                       [0., 257.08, 0.],
                       [0., 151.03, 0.],
                       [0., 278.88, 0.],
                       [0., 251.73, 0.],
                       [0., 0., 0.],
                       [0., 0., 100.],
                       [0., 137.5, 0.],
                       [0., 0., 0.]])

    expmapInd = np.split(np.arange(4, 100) - 1, 32)

这几组数据定义了骨骼数据的结构以及对应的旋转向量下标:

parent[i]表示第i个关节点与它的父节点组成的骨骼向量的旋转矩阵的索引地址；

offset[i]表示了在初始模型中骨骼向量parent[i]-i的长度和方向；

expmapInd[i]表示了各个旋转向量在标注数据中的分组，其中有99个数据中的下标，代码中每三个分一组，可以看到下标从3开始，因此前三个数据也就是第一个向量并未使用，总共分为32组。
————————————————
版权声明：本文为CSDN博主「alickr」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/alickr/article/details/107837403